이동경로는 반드시 시점과 종점을 초점으로 가지는 타원안에 존재하게 된다.

이동거리와 초점을 이용해서 단축의 거리를 알아낼 수 있다.

타원의 방정식을 통해 단축의 값을 이용해 장축을 알아낼 수 있다.

이동거리가 시작점과 종점사이의 거리와 정확히 일치하는 경우, 경로는 1가지

시작점과 도착점이 같은 경우 시점(종점)을 중심으로 하는 이동거리 절반을 반지름을 가지는 원을 그리게 된다.

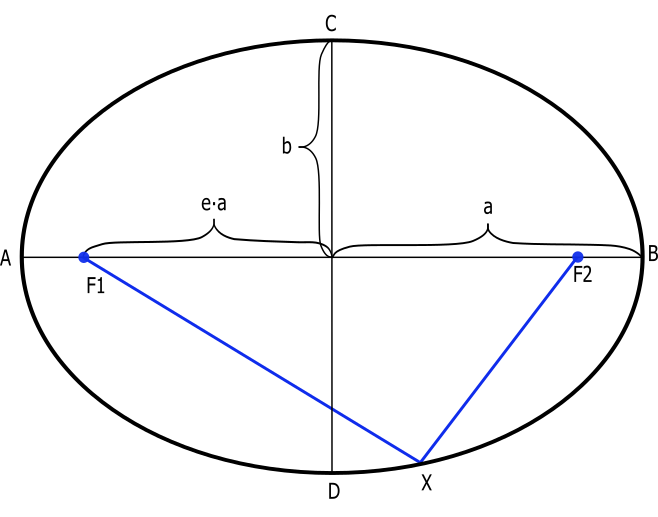
이 외의 경우에는 타원내에 경로가 생성된다. 

이심률을 이용해서 직선AB에서 C(D)가 어느정도 떨어져 있는지 계산한다.(위에서 계산한 단축의 거리는 단축 거리가 최대일 때 이다.)

단축의 거리를 제한함으로써 경로는 좀 더 직선 AB에 가까워지고 이는  조금 더 경로예측을 하는데 도움을 준다.

맨위의 사진은 이러한 시점 종점을 연달아 이어 붙인 것이다.

파란 궤적을 각 포인트와 그 사이의 이동거리를 기록한다면 타원 범위 안에서 경로를 예측할 수 있다. 또한 시점 종점 수평 선상(직선 AB)에서 얼마나 벗어나는지에 대한 통계데이터를 이용해 경로의 예측 확률을 높이는 것이 가능하다.

지도 데이터(MAP레이어)와 결합해서 가지 않은 곳을 확인해 그 지역에 추가적인 조치를 취하거나 도로에 적용한다면 유용하게 사용할 수 있다.  

또한 꼭 지나야 하는 지점을 타원 내 지점으로 설정할 경우 최적의 이동 경로를 뽑아 낼 수 있어 효용성이 있어 보인다.